第一 代入法
常用题型:多位数问题、不定方程问题、余数问题、年龄问题、复杂行程问题等
最值代入
直接代入选项时,若题目要求的是“最多/最大”时,代入选项应从最大的数开始;若题目要求的是“最小/最少”时,代入选项应从最小的数开始。(如是确定的不定方程,个人觉得应该倒数第二个数开始)。
居中代入
直接代入选项时,若选项中的数据为从小到大的均匀数字,一般选择大小居中的进行代入。若结果不正确,分析大小趋势选择下一个代入项。
数字特性
常用的数字特性有奇偶性、整除、尾数等。根据题目中的条件,确定答案数字所具有的某种数学特性,排除不符合特性的选项。
常识代入
不通过具体计算,只运用一定的常识,从而直接排除某些选项的方法。例如:若两种溶液混合后得到的浓度为10%,那么可得一个浓度大于10%,一个小于10%,从而可排除不符合要求的选项。
第二 整除判断法
常用题型:分数、比例、倍数、整除等明显特征,此时一定要考虑整除判断。
特殊数字整除判断
2/5 :末尾数能否被 2/5 整除
4/25 :末尾数两位能否被 4/25 整除
8/125 : 末尾数三位能否被 8/125 整除
3/9 :其各位数字之后能否被 3/9 整除
普通数字的判断
一般采用分解因式的方法进行快速判断。
分数比例形式
如 a :b = m : n (m / n 互质),则a是m的倍数,b是n的倍数;若 $a=\frac{m}{n} \times b$(m、n互质),则a 是m的倍数,b是n的倍数。
要有观察选项的能力
例:(2017年广东)某批发市场有大小两种规格的盒装鸡蛋,每个大盒里装有23个鸡蛋,每个小盒里装有16个鸡蛋。餐厅采购员小王去该市场买了500个鸡蛋,则大盒装一共比小盒装()
A. 多2盒 B. 少1盒 C. 少46个鸡蛋 D. 多52个鸡蛋
解:找关系,列方程,把最终要需要的答案的方程要列出来,观察选项判断;
点题:$a + b = c$ 如果a被c整除则b被c整除;如a不被c整除则b不被c整除
第三 奇偶性
出现$ax + by = c$的等量关系,考虑能否使用奇偶特性法,多用于不定方程求解
$2n = 偶数$
$2n + 1 = 奇数$
注意:逆向思考,和为偶则两项必同奇或同偶;和为奇则必一奇一偶。
如果不定方程式子较多时,根据奇数的个数判断和奇偶性。
例:(2009年浙江)现有6个一元面值硬币正面朝上放在桌子上,你可以每次翻转5个硬币(必须翻转5个),问你最少经过几次翻转可以使6个硬币全部反面朝上?()
A.5 B.6 C.7 D.8
解:每个硬币必定翻转奇数次,总次数等于六个奇数之和,为偶数,因A/C项为25/35次,故排除;每次只能翻5个,每个硬币翻转的机会均等,得每个硬币翻转的次数为$x = \frac{5 \times n}{6}$,x为奇数,所以n必整除6,选B
例:小李用150元钱购买了16元一个的书包、10元一个的计算器和7元一支的钢笔寄给灾区儿童。如果他买的每一样物品的数量都不相同,书包数量最多而钢笔最少,那么他买的计算器数量比钢笔多几个?()
A.1 B.2 C.3 D.4
解:设书包x、计算器y、钢笔z,得
$16x + 10y + 7z = 150 \tag{1}$
由(1)得出,z为偶数,设z=2代入计算,由尾数原则x=6,代入(1)计算的y=4,选B
第四 赋值法
题干中出现了分数、比例、倍数时,要考虑赋值法。多用于分数应用题、工程问题、行程问题以及费用问题等。
基本原则
- 题干中数据没有单位,只有比例关系时,可以使用赋值法简化计算。
- 题干中的数据有单位,但是单位只有一种,且与其他数据有比例关系时,可以使用赋值法简化计算。
- 题干中出现了分数,赋值的基本原则是赋整数,所赋数字为分母的倍数。有多个分数的话,赋值为分母的最小公倍数。
- 题干中出现的是数量之间的比例关系,那么根据比例关系,进行整数赋值。
第五 工程问题
$工作量 = 工作效率 \times 工作时间$,其中工作效率是工程问题的核心。
常用解法有赋值法、代入法以及列方程求解
一般情况下,一道题不能单用一种方法解决,而是多种办法的结合。优先考虑列方程,再赋值或者代入选项法。
例:(2016年4月联考)A工程队的效率是B工程队的2倍,某工程交给两队共同完成需要6天。如果两队的工作效率均提高一倍,且B队中途休息了1天,问要保证工程按原来的时间完成,A对中途最多可以休息几天?()
A.4 B.3 C.2 D.1
解:$工作效率 \times 工作时间 = 工作量$,工作量和工作效率都未知,且无单位,故设B的工作效率1/天,因为A:B的效率比是2:1,优先设B为1,如果设A为1,B为0.5不利于计算,赋值法优先考虑利于计算的整数。故得工作总量 = 18.
列方程最好通过图像和列表结合,理清各项关系:
解得x = 2,则A休息4天答案选A项
第六 尾数法
尾数法适用的运算:加法、减法、乘法以及乘法运算。
应用题:数字类计算题,容斥原理等。
- 选项尾数不同,且运算过程为加、减、乘、次方运算,优先使用尾数进行判断;原因:尾数为确定的,除法尾数不一定确定
- 所需计算数据多,计算复杂时考虑尾数判断快速得到答案;注意观察选项的尾数是否相同,如果都不同运算准确率高。
- 注意尾数所对应数位,避免小数运算尾数为0而带来的风险
- 除法运算需转换为乘法运算后,才能进行尾数判断
- 求$A^n$的个位数,指数处除于4留余数,余数为0,取4次方,次方尾数有周期性。如:$1997^{1997} \rightarrow 7^1$,得尾数为7
例:(2007年北京)计算$(873\times477-198)\div(476\times874+199)$的值是()
A.1 B.2 C.3 D.4
解:尾数法,$873\times477-198=(476\times874+199)\times答案$;左边尾数为3,故右边尾数为3,代入1成立,选A项。
解法二:估算法,$873\times477 和 476\times874$大小差不多,且远大于198和199,因此分子和分母大小相当,故选A项。
第七 裂项相消
$\frac{b}{m\times(m+a)}=\frac{b}{a}\times(\frac{1}{m}-\frac{1}{m+a})$
题干为多个分式或分数相加,各项分母可表示成两数或多数相乘,考虑裂项相消。
- 两项分母裂项:
- 三项分母裂项:
例:$2008\frac{1}{18}+2009\frac{1}{54}+2010\frac{1}{108}+2011\frac{1}{180}+2012\frac{1}{270}=()$
A.$10050\frac{5}{54}$ B.$10052\frac{7}{135}$ C.$10051\frac{269}{270}$ D.$10051\frac{1}{54}$
解:A
第八 等差数列
- 求和:$和=\frac{首项+末项}{2}\times项数=平均数\times项数=中位项\times项数$
- 级差:$第N项-第M项=(N-M)\times公差$
- 项数:$项数=(末项-首项)\div公差+1$
- 对称公式:若$m+n=i+j \Rightarrow a_m+a_n=a_i+a_j$
- 奇数求和:$1+3+5+7+\cdots+(2n-1)=n^2$
第九 约数倍数
$A=a \times b \times c \text(A是a、b、c的公倍数,a、b、c为A的约数或因数)$
- 题干中出现了“每隔······”、“每经······”等含“每”的字眼时,经常要考虑最小公倍数;
- 当题目要求对定长进行等分,求“最小”的段数、植树的颗数或安装物体的数量等,要考虑最大公约数。
两数的求解
分数的最大公约数
分数的最小公倍数
每隔 x,则周期为 x+1
第十 余数问题
$被除数 = 除数\times商 + 余数(0\leq余数<除数)$
同余问题
就是给出“一个数除以几个不同的数”的余数,反求这个数,称作同余问题. 首先要对这几个不同的数的最小公倍数心中有数,下面以4、5、6为例,请记住它们的最小公倍数是60.
- 差同减差:
用一个数除以几个不同的数,得到的余数,与除数的差相同, 此时反求的这个数,可以选除数的最小公倍数,减去这个相同的差数,称为:“差同减差”.
例:“一个数除以4余1,除以5余2,除以6余3”,因为4-1=5-2=6-3=3,所以取-3,表示为60n-3.
【60后面的“n”请见4、,下同】 - 和同加和:
用一个数除以几个不同的数,得到的余数,与除数的和相同, 此时反求的这个数,可以选除数的最小公倍数,加上这个相同的和数,称为:“和同加和”.
例:“一个数除以4余3,除以5余2,除以6余1”,因为4+3=5+2=6+1=7,所以取+7,表示为60n+7. - 余同取余:
用一个数除以几个不同的数,得到的余数相同, 此时反求的这个数,可以选除数的最小公倍数,加上这个相同的余数,称为:“余同取余”.
例:“一个数除以4余1,除以5余1,除以6余1”,因为余数都是1,所以取+1,表示为60n+1. - 最小公倍加:
所选取的数加上除数的最小公倍数的任意整数倍(即上面1、2、3中的60n)都满足条件, 称为:“最小公倍加”,也称为:“公倍数作周期”.
余数特性
- 余数可加性:
a与b的和除以c的余数,等于a、b分别除以c的余数之和。 - 余数可减性:
a与b的差除以c的余数,等于a、b分别除以c的余数之差。 - 余数可乘性:
a与b的乘积除以c的余数,等于a、b分别除以c的余数之积。
注:当余数之积(和或差)大于除数时,所求余数等于余数之积(和或差)再除以除数的余数。
第十一 周期规律
核心在于根据题型找出规律,常见的有余数、尾数成规律,排列成规律,题干的描述呈现等差、等比或周期数列变化等,解题方法有枚举法、归纳法等。
常考题型:
- 数字计算类:
分数类计算题可以采用裂项法进行消去;较高幂次的尾数可直接根据乘方尾数公式;其他类计算题采用分组找规律的方式。 - 排列组合类:
几何计数类,从基数小、较简单的入手,采用枚举归类法,找规律。 - 排列组合类:
新颖的排列组合题目往往考查规律归纳的能力,通过枚举逐步分析。 - 日期计数类:
年365天,月30天,星期7天。
例:
- 用四种颜色对下图中的A、B、C、D、E五个区域染色,要求相邻的区域染不同的颜色,共有()种不同的方法。
A.80 B.96 C.108 D.120
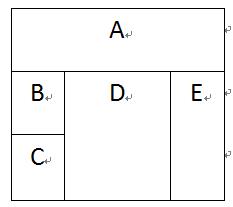
解:用直接列举的办法,可以从接触面最多的D开始,D,E,A,B,C开始染色,注意色彩可以重复只要不相邻即可,共有$4 \times 3 \times 2 \times 2 \times 2 = 96$选B
- 甲、乙、丙三人从星期一开始工作,甲每工作3天就休息一天,乙每工作5天就休息一天,丙每工作7天就休息3天,那么三人第一次同时休息是在星期几?()
A.星期三 B.星期四 C.星期六 D.星期日
解:直接列举解答,得到星期六
第十二 不定方程问题
常用技巧:偶数特性、整数特性、尾数特性、赋值代入,以及整体消去等方法。
不定方程指未知数的个数大于方程的个数,且未知数受到某些限制(要求整数、质数、奇偶等等)
- 二元不定方程:
$ax + by = c$
利用奇偶特性或整除特性进行求解,要结合选项赋值代入
如:$12x + 5y = 99(x + y > 10,且x、y为整数)$12
解:12x为偶,99为奇,所以5y一定是奇数,得出y为奇数,则5y尾数为5,12x的尾数必定为4。假设x=2,得y=15,符合题意。 - 多元不定方程:
整体消去,特值代入法等
如:整体消去:$3\times(1) - 2\times(2)=x+y+z=3 \times 72 - 2 \times 86 = 44$
特值代入:设x=0,得y=7,z=37,故x+y+z=44
第十三 溶液问题
基本公式:
- 溶液混合问题:
两溶液混合,质量分别为$M_1 、M_2$,浓度分别为$C_1、C_2$,混合后溶液浓度为C,则公式:
$M_1C_1 + M_2C_2 = (M_1 + M_2)C$
第十四 十字交叉法
- 溶液混合问题:
两种不同浓度的溶液混合,得到混合浓度大小居中,十字交叉得到的比例为”混合前溶液的质量之比或体积之比”。 - 平均数混合:
两组数据混合,得到的混合平均数大小居中,十字交叉得到的比例为”两组数据的数量之比”。 - 增长率混合:
总量的两个分量增长率混合,得到的混合增长率大小居中,十字交叉得到的比例为”两个分量的基期量之比”。 - 利润率混合:
两个不同利润率的商品混合,得到的混合利润率大小居中,十字交叉得到的比例为”两种利润率混合前所对应商品的销量之比”。 - 折扣混合:
两种不同折扣的商品混合,得到的混合折扣大小居中,十字交叉得到的比例为“混合前所对应商品的总价之比”。
第十五 相遇追及
公式:
认真审题区分是相遇还是追及问题,注意“相向”、“背离”、“同向”等字样
- 环形运动问题:
同一点方向运动:$环形周长=(大速度+小速度)\times相遇时间$(第一次相遇)
同一点同向运动:$环形周长=(大速度-小速度)\times相遇时间$(第一次相遇) - 直线往返相遇问题:
左右点出发:第N次迎面相遇,$路程和=全程\times(2N-1)$ 。
同一点出发:第N次迎面相遇,$路程和=全程\times 2N$;第N次追上相遇,$路程差=全程\times 2N$ 。 - 队伍行进问题:
第十六 钟表问题
时钟表盘分12大格,每格$30^0$,时针转速为$0.5^0/分$,分针转速$6^0/分$。
分针与时针一昼夜重合22次,成直角44次,成$180^0$角22次。
第十七 比例法
第十八 调和平均数
调和平局数公式:
$\overline{a}=\frac{2a_1a_2}{a_1+a_2}$ ,本质在于$\frac{1}{a_1} , \frac{1}{ \overline{a} } , \frac{1}{a_2}$成等差数列
- 等距离平均速度:$v_1与v_2$所经历的路程相同,求平均速度$\overline{v}=\frac{2v_1v_2}{v_1+v_2}$。
- 等间隔发车时间:$t_1与t_2$所经历的路程相同,求发车相隔时间$t=\frac{2t_1t_2}{t_1+t_2}$。
- 等费用平均价格:$p_1与p_2$所消耗的费用相同,求平均价格$\overline{p}=\frac{2p_1p_2}{p_1+p_2}$。
- 等溶质增减浓度:$r_1与r_2$所蒸发的溶剂相同,求中间一次浓度$r=\frac{2r_1r_2}{r_1+r_2}$。
第十九 牛吃草
核心:$Y=(N-X)\times T$
第二十 年龄问题
核心:$\color{red}{年龄差恒不变}$
第二十一 经济利润问题
基本概念:
- 进价成本:商家买入的价格
- 售价:实际卖出货物的价格
- 利润=售价-成本:商家赚到的钱
- 折扣:2折即为原价的20%,9折为原价的90%
基本公式:
- $利润率(加价率/加价幅度)=利润\div成本=(售价-成本)\div成本=售价\div成本-1$
- $打折后的售价=原售价(定价)\times折扣$
- $总利润=总收入-总成本=单利润\times销量$
第二十二 容斥原理
思路:先不考虑重叠情况,将所有集合的数目加和,然后再逐步“去重”
- 两集合公式:$A\cup B=A+B-A \cap B$
- 三集合公式:$A\cup B\cup C=A+B+C-A\cap B-B\cap C -C\cap A +A\cap B\cap C$
$\color{red}{注:画图帮助思考}$
第二十三 排列组合
分类用加法原理,分步用乘法原理;
考虑顺序用排列,不考虑顺序用组合。
概念:
- 分类是指对完成一件事,需要划分几个类别,各类别内方法可以独立完成该事;
- 分步是指对完成一件事,需要分为几个步骤,每个步骤内的方法只能保证完成该步。
思路:
- 加法原理:各类别方法总数相加。
- 乘法原理:各步骤的方法数目相乘。
- 排列公式:$A_n^m=\frac{n!}{(n-m)!}=n\times(n-1)\times(n-2)\times \cdots \times(n-m+1)$
- 组合公式:$C_n^m=C_n^{n-m}=\frac{n!}{n!(n-m)!}=\frac{n\times(n-1)\times(n-2)\times \cdots \times(n-m+1)}{m\times(m-1)\times(m-2)\times\cdots\times1}$
- 环形排列:n个人排成一圈,有$(A_n^n \div n)$种排法;n个珍珠串成一条项链,有$(A_n^n \div 2n)$种串法。因为珍珠串的空间坐标和人不一样,珍珠串可以翻转180度,但是人圈却不能,所以注意差别。
- 错位排列:有n封信和n个信封,每封信都不能装在自己的信封里,可能的方法为$D_n,D_1=0,D_2=1,D_3=2,D_4=9,D_5=44,D_n=(n-1)(D_{n-2}+D_{n-1})$
第二十四 捆绑插空
相邻问题考虑捆绑;不相邻问题考虑插空。
- 捆绑法:6个人站一排,要求甲、乙必须相邻,则一共有()种排法。甲乙看成一个整体,和剩余4人全排列,共$A_5^5$;另外甲乙排序有$A_2^2$,则有$A_5^5 \times A_2^2=240$种排法
- 插空法:6个人站一排,要求甲、乙必须不相邻,则一共有()种排法。除甲、乙外,4人有$A_4^4$排法,再把甲、乙插入4人产生的5个空中(包括两端),有$A_5^2$,则有$A_4^4 \times A_5^2=480$种排法
第二十五 抽屉原理
最不利原则:考虑对于需求满足条件的“最不利”情况,结果为“最不利+1”
题干中出现“至少······,才能保证······”等信息。
第二十六 构造设定
总量一定,一个量要想最多(最少),则其他量最少(最多)
第二十七 三边关系
- 在三角形中,两边之和大于第三边,两边之差小于第三边。
- 直角三边形中,直角边平方之和等于斜边平方
特殊勾股数
| 直角边 | 3 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| 直角边 | 4 | 12 | 8 | 24 | 15 | 12 |
| 斜边 | 5 | 13 | 10 | 25 | 17 | 15 |
| $x \times y$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
第二十八 几何面积
面积一定,越接近于圆,则周长越小;周长一定,越接近于圆,面积越大。
一个几何图形尺寸为原来的n倍,面积为原来的$n^2$倍,体积为原理的$n^3$倍。
第二十九 几何体积
体积一点的图形,越接近于球,则表面积越小;表面积一定的图形,越接近于球,则体积越大。
第三十 植树问题
- 单边线型植树(两头植树)颗数=总长$\div$间隔+1
- 单边楼间植树(两头不植树)颗数=总长$\div$间隔-1
- 单边环形植树:颗数=总长$\div$间隔
- 双边植树:总数=单边颗数$\times$2
第三十一 方阵问题
相邻两层单边数量相差为2
相邻两层外层人数比内层人数多8人
实心方阵总人数是平方数
实心方阵:
N排N列的方阵
总人数=$N^2$
最外层人数=$4N-4$
M排N列的长方阵
总人数=$M\times N$
最外层人数=$2M+2N-4$
空心方阵(中空方阵):
总人数=大实心方阵人数-小实心方阵人数=(最外层人数+最内层人数)$\times层数\div2$=中间层人数$\times$层数
层数=(最外层人数-最内层人数)$\div8+1$
中间层人数=(最外层人数+最内层人数)$\div2$
第三十二 过河爬井与空瓶换酒
M个人过河,船上能载N个人,需要1人划船,则共需过河$\frac{M-1}{N-1}$次
M个空酒瓶换1瓶酒,相当于(M-1)个空瓶可以喝到一瓶酒。
过河问题中,需要注意的是需要几个人划船,是单程还是往返。
将“M个空瓶换N瓶酒”转换为“(M-N)个空瓶换N个(无瓶)酒”来解题。
- 过河问题:M个人过河,船上能载N个人,需要n人划船,则共需过河$\frac{M-n}{N-n}$次,且最后一次是单程,其他为往返运动。
- 空瓶换酒问题:若原有M瓶酒,N个空瓶换1瓶酒,则$新换瓶数=\frac{M}{N-1}$(取整数)。
- 变形题,青蛙爬井问题:井的深度为M,青蛙每天爬N,每次下滑x,则青蛙从井中跳出的天数为$\frac{M-x}{N-x}$。
第三十三 对折与倍增
- 一根绳子对折N次,剪M刀,得到$M \times 2^N+1$段绳子。
- 如果一个量,每个周期后变为原来的A倍,那么n个周期后就是最开始的$A^n$倍,一个周期前应该是当时的$\frac{1}{A}$。
对折和倍增本质是等比数列。
第三十四 统计术语
术语1.基期量与现期量、增长量与增长率
术语2.同比和环比
同比是默认比,是指与上年同期相比;
环比会明确告知,是指与上一个统计周期相比。
如:第三季度增长10%,则和去年的第三季度相比;第三季度环比增长10%,则和第二季度相比。
术语3.比重
- 比重:比重是指部分在整体中所占的比例
- 基期比重计算:若某部分的现期量为A,增长率为a,整体的现期量为B,增长率为b,则基期的某部分占整体的比重为$\frac{A\div(1+a)}{B\div(1+b)}$,化简后得$\frac{A}{B}\times \frac{1+b}{1+a}$
术语4.拉动增长率与增长贡献率
如果B是A的一部分
- B对A的拉动增长率是指B的增量与A的基期量的比值。
- B对A的增长贡献率是指B的增量与A的增量之间比值。
术语5.平均增长率
平均增长率:某量初期为A,经过n个周期之后变成B,平均增长率为r,则$A(1+r)^n=B$
平均增长率近似公式:当$\left|r\right|<5\%$ , $(1+r)^n=1+nr$
第三十五 八大速算法
1.估算法与直除法
当选项相差较大,或者被比较数据相差较大,且运算过程较复杂或计算式较复杂时,采用估算法。
估算法:
- 估算法是为了简化计算采用的近似取整计算;
- 除法估算的原则是分子分母同大同小,乘法估算的原则是一大一小;
- 估算法经常会涉及数位的截取,一般选择保留前三位有效数字。
直除法:
直接相除,若选项前两位不同,选择直除法
2.化同发与放缩法
比较分母大小时,化同法是将分子(或分母)化至完全相同或相近的方法,再进行比较;
放缩法是将其中一项或中间结果适当地放大或缩小,实质为就近取整,再进行比较的方法。
比较两个分数大小:
- 化同法:
- 放缩法:比较分数A和B大小,可以将A或B放大或缩小,寻求一个中间量,如将A放大C,即A<C,若C<B,则A<B。
3.插值法与差分法
比较A和B的大小,若可以找一个数x,满足A>x,而且B < x, 则可以判定 A>B
差分法利用”差分数”替代“大分数”与“小分数”比较。
- 插值法:一般选用$\frac{1}{3} \frac{1}{4} \frac{1}{5} \frac{1}{6} \frac{1}{7}$ 例如:计算$\frac{3281.3}{13057.2}$,选项中有25.13%和24.87%,中间项为0.25,而$3281.3\times 4=13125.2>13057.2,所以\frac{3281.3}{13057.2}>0.25$,则选25.13%
- 差分法:把$\frac{A+\Delta A}{B+\Delta B}$称为大分数,$\frac{A}{B}$称为小分数,分子、分母作差得到新分数$\frac{\Delta A}{\Delta B}$为差分数。若 差分数>小分数,则大分数>小分数;同小或等同。
4.凑整法与公式法
凑整计算:
增长率逆推公式:
如果现期量A,相对基期的增长率为a%(a<5),则基期$A_0=\frac{A}{1\pm a\%} \approx A\times (1\mp a\%)$比真实值偏小。增长率的展开式:$(1+x\%)^n \approx 1+nx(x<5)$比真实值偏小。
第三十六 七大题型
1.$\frac{A}{B}$
基期量计算、比重计算、平均数计算、倍数计算、增长率计算,均为$\frac{A}{B}$
2.$\frac{A}{B}\times C$
特殊分数:
- 增长率计算:
3.$\frac{A}{B}\times\frac{A}{B}$
基期比重计算:
部分现期量A,增长率a%,整体现期量B,增长率b%;
$基期部分占整体的比重=\frac{A}{1+a\%}\div\frac{B}{1+b\%}=\frac{A}{B}\times\frac{1+b\%}{1+a\%}$
由此判断A相对B现期比重和基期比重变化
4.$\frac{A}{B}-\frac{C}{D}$
5.增长量大小比较
6.增长率大小比较
灵活使用估值法、直除法、插值法、放缩法
7.比重大小的比较
| $x^{y}$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||||
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | |||||
| 4 | 16 | 64 | 256 | ||||||
| 5 | 25 | 125 | 625 | ||||||
| 6 | 36 | 216 | |||||||
| 7 | 49 | ||||||||
| 8 | 64 | ||||||||
| 9 | 81 | ||||||||
| 11 | 121 | ||||||||
| 12 | 144 | ||||||||
| 13 | 169 | ||||||||
| 14 | 196 | ||||||||
| 15 | 225 |
Description: page.date
Copyright:署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

